3.17 Process

Process is another mathematical element closely related to life. You do not have to look far for examples: the process of raising children, the steel production process, the process of cellular multiplication, the process of the development of life on Earth, etc. Although processes are surrounding us on all sides and, recently, this term is in common use, the mathematical meaning is known only by a few. It is only taught in a few faculties in a few technical universities. Mathematically, the issue is quite complex, and discussing it precisely would double the size of this book. So we will only give the essentials, yet the absolute minimum of knowledge about it.

3.17.1 Process – two definitions

Process, unfortunately, is an ambiguous term. For the physics of life, the most important are the two following definitions: mathematical (stability theory), according to which a process is the sequence of consecutive states of a given system's property; and economic - anything that produces a specific service or product. So the differences between these two definitions are quite substantial, but both are needed. According to the first definition, a process is passive - it only informs about the behaviour of a system over time; while according to the second, it is active and targeted (for example, machining, the educational process or the process of biological evolution). So, the first definition states that the process is a sequence of changes in the property of a system, and the second states that a group of causal factors cause these changes in a characteristic way. The word "process" is commonly used in both of these meanings and often misleading, however, we have to precisely distinguish both terms. Processes play a fundamental role in the physics of life processes so in order to avoid ambiguity we will state which process we will use.

Definition of behaviour according to the physics of life
Whenever we discuss behaviour of a system we will consider it in it's mathematical sense. Behavoiur of a system in the physics of life means "the changes of the states of all its properies over time".

3.17.2 System’s behaviour

Definition of initial conditions
An object/system is characterized by the set of its properties, and each of them has its temporary state which can vary over time. This variability is the behaviour of the system, or, in other words, the process in its mathematical sense. Each system behaves in a certin way when left alone. The changes may not be apparent, but it is still a behaviour of the system. We say that the system is in it's equilibrium. Consider a general situation when the state of a given property of a system changes over time. Usually, in physics, the symbol t_s denotes the starting point of an observation. Let us define the state of a system according to the state of all of its properties. Consequently, the starting state of a system is the state of all its properties at t_s. Imagine a car driving from Paris to Pamplona, via Madrid. The t_s is when the driver gets into the car near Champs-Elysees and starts the engine. We will focuse on one property of the car - velocity. At t_s its state is zero. Several hours later, the car drove through Pamplona at 50 km/h without stopping. This could also be considered as a t_s, but of a slightly different system - the car travelling from Pamplona to Madrid with an initial speed of 50 km/h. Any system can be considered different according to the initial point of observation.

Influnence of disturbances on the behaviour of a system
Let's create a mental experiment. We have a system with a given set of initial conditions. If we leave it, the system will behave in a given way, which means that its properties will change their state over time in a given way. Now, if we repeat this excperiment with exactly the same system and exactly the same initial conditions, the behaviour will be exactly the same. This experiment was performed in mathematical space, where everything could be repeated in exactly the same way. What differs mathematical space from physical space is the word "exactly". In real life - physical space - we can never repeat anything in exactly the same way. There are always some differences, sometimes these differences are infinitesimally small, but they still exist.

Let us now move from the "clean and perfect" mathematical space to the "dirty and devious" physical space. Unfortunately, we cannot repeat any experiment in exactly the same way in physical space⁴³. Firstly because we cannot obtain exactly the same conditions, and secondly because the system changes after each use. This observation is so important that it should be called the axiom of unique behaviour. This axiom forces us to analyze how the infinitesimally small changes of either the initial conditions or the system itself can influence its behaviour.

In the next section we will present the basic element of stability theory, which is not taught in schools nor in the vast majority of universities, yet it is of the utmost importance when trying to understand life.

3.17.3 Three characteristic types of systems

When someone speaks about equilibrium, most people immediately think about its three states: stable, unstable and neutral. There is a similar classification with systems and their behaviours. To understand this, let us analyze the behaviour of a hypothetical system that has only one property named ε. Its initial condition is ε(0)=ε_p. Now we leave the system recording its behaviour.

Figure 33. Behaviour of the system

The state of the property measured over time illustrates the curve ε(t), which is represented in figure 33 by the blue line. What happens when we try to duplicate the experiment? According to the axiom of unique behaviour, we are unable to recreate exactly the same initial conditions.

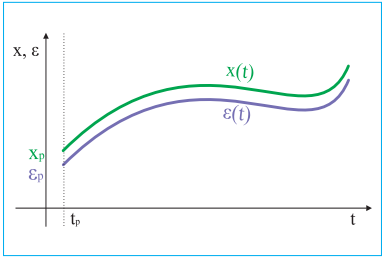Figure 34. Behaviours of a stable system

So now we will see how this change will influence the behaviour of the system. One of the possible behaviours is shown in figure 34 as line x(t). As you can see, the only difference from the original - ε(t), is that the lines have shifted slightly. It can be assumed that the system has behaved in a similar way.

With repetition, always having in mind that every time we slightly change the initial conditions and that the system also changes with use, we still observe that its behaviour does not change its characteristics, so we can say that the system behaves similarly. Scientists who studied the issue of process-behavior, such as the Russian physiomathematician Alexander Lyapunov (1857 -1918), called such systems stable. Mathematical definitions of stability are quite complicated and, although mathematicians will complain, I will provide a simplified version. A system is considered to be stable if it, when left alone in an initial state, sufficiently close to the original initial state, behaves sufficiently similarly to the original behaviour. I can almost see astute readers jumping from their chairs, asking indignant questions: "Why, in a pure mathematical definition, are you using adverbs and adjectives? And what does "sufficiently close" and "sufficiently similarly" mean?! Please do not cry. When people use adjectives, it means that they are needed for some reason. Mathematicians are clever and are even able to precisely define some adjectives. For example, "sufficient closeness" has been defined by using limits of sequence and convergence. However, in order not to complicate the discussion, assume that "sufficiently close" is also a mathematical concept. The point is not to argue and split hairs, but to remember the concept of the stable system, one that when you slightly change the initial conditions behaves more or less similarly to the original.

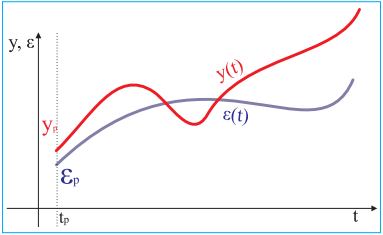Figure 35. Behaviours of an unstable system

Now imagine a different system. This time you will see that the behaviour of the system, eg. y(t), although it was started in similar initial conditions, behaves very differently from the original ε(t). Moreover, the course of each subsequent behavior is different from the previous ones. These systems are named unstable. It is worth noting that the system is vulnerable to changes in the initial conditions. It is a far-reaching conclusion worth remembering. Even small differences can radically change the behaviour of a system.

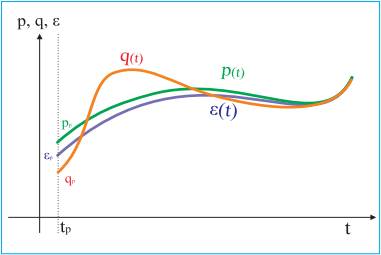Figure 36. Behaviours of an asymptotically stable system

Let's examine another system. ε(t) in figure 36 represents the initial behaviour. We can see that even being initailly different, the behaviours p(t) and q(t) finally converge with ε(t). Over the passage of time, the system behaves in the same way regardless of the initial conditions. We call such systems asymptotically stable. There is a rule of thumb to distingush between those three systems: the behaviours of stable systems lie in "a tube", asymptotically stable systems lie "in a funnel" and unstable ones go everywhere!

3.17.4 Impact of disturbances on behaviour

The behaviour of a system is a sequence of system states occurring one after the other. So at a given time, the state of a system not only depends on its properties, but also on its previous state. Each future state depends on it predecessor. In short, the present state of a system depends on its properties and the history of its previous states. Let us now introduce the concept of disturbance. Disturbance can be defined as a random change of a state of a property of a system. The reason for this change does not have to be specified.

Figure 37. Influence of disturbances on the behaviour of the system

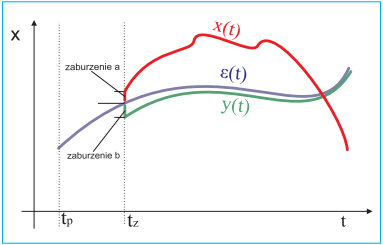Suppose that the system is disturbed at t_z. This moment can be considered as the initial condition for further observation. And now let's recall everything we talked about a moment ago. If the disturbance does not occur, the behaviour of the system will be ε(t). We can see that disturbance A caused, unfortunately (or fortunately), the behaviour x(t). We can also imagine that a different disturbance, B, caused a different behaviour y(t). Depending on the system, disturbances can have different effects on its behaviour. As shown in figure 37, the change can either be significant, as x(t), or insignificant, as y(t). In the former, we are talking about vulnerable (or sensitive) systems, and in the latter, invulnerable.

Figure 38. Influence of disturbances on a system

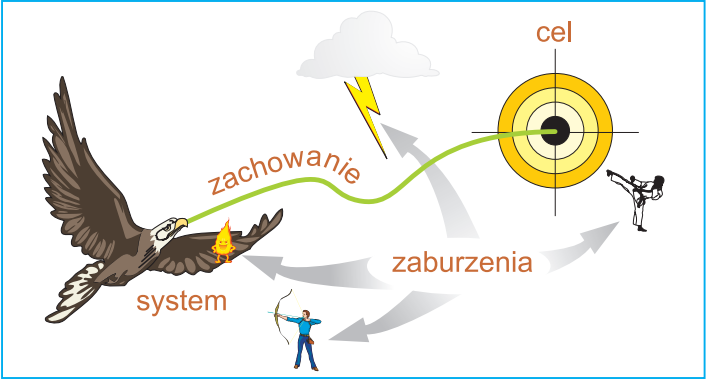Let's look at disturbances in the real world. The yellow imp symbolizes the disturbance within the system (sudden abdominal pain, blurring of vision), archer - external disturbances influencing the system (shooting down, injury), lightning - external disturbances affecting behaviour (air pressure), and unforeseen events like a ninja - an external disturbance that can change the purpose (nest under attack). Disturbances can be divided into the predictable, such as a puncture during a long trip, and unpredictable. In the latter case it is even difficult to provide a meaningful example.

Figure 39. Comparison of balance and stability concepts

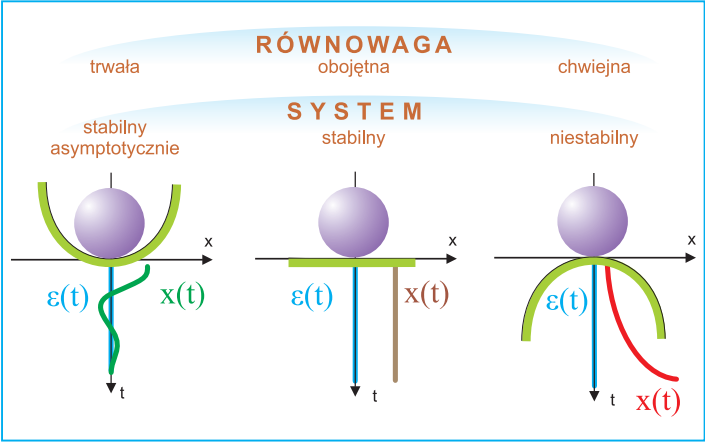Now let's compare balance with stability. Look at these three balls located on different surfaces. The ball in the concave surface is an asymptotically stable system with one defined point of equilibrium, which does not vary over time. After any disturbance, the system "pushes back" the ball to this position of equilibrium. The cause of this (the causative factor) is a negative feedback mechanism. The ball on the flat surface has multiple stable positions of equilibrium. After it has been moved from its original position by a disturbance, the ball remains stable in a new position. The ball on a convex surface is an example of an unstable system, vulnerable to the slightest disturbance.

3.17.5 Study of behaviours, study of processes

Let's return to the definitions of a process: a process, in its business meaning, is a set of factors resulting in a final product. A mathematical process is a sequence of successive states of a systems properties, its behaviour. When we know the basic classification of systems, let's see how mathematicians study them? The most important assumption is that the any observed behaviour will never happen again - the Second World War has already happened and will never happen again. The only thing we can study is its history - its behaviour - and we can draw some conclusions. However, if we want to study war as a system, we need to create a model and study the behaviour of this model. In other words, we do not study the behaviours of the system, because they are unique, but the factors generating them. In order, therefore, to predict how a particular real system will behave, we need to build its model and examine the impact of various factors which can impact on its behavior. Only then can we try to predict anything in relation to the expected behavior of the real system. Theory of systems is the scientific discipline which build such models and study them, which is one of the elements of cybernetics.

Someone might ask, "How do I investigate the behaviour of a system, having never built models or studied cybernetics?". A table with two columns, one column listing all the constructors and the other listing all the destructors may be considered as the simplest tool to imagine how a system might behave. However, in personal judgments we need to be extremely careful because our highly biased intuition may lead to negative results⁴⁴. We do not realise how many times our intuition can be wrong. Due to this, it is highly advisable not to rely on your intuition, but rather on the laws of physics and objective observations. Let's see how such a table might look for our example of a ball in a hole. The initiator is the placement of the ball on the concave surface. The constructors of the asymptotically stable process are any factors that maintain the concavity of the surface and its proper orientation relative to gravity. In reverse, the destructors are the factors which lead to the concavity becoming convex or turning the surface upside-down, so that the ball pops out.

3.17.6 Some typical processes

Another method to study processes is to find the analogy between what is being studied and some typical processes - well described standards - such as, for example, a chain reaction.

3.17.6.1 Chain reaction processes

3.17.6.2 Inevitable processes

3.17.6.3 "Random accummulation of innocent factors leading to disaster" processes

3.17.6.4 "Ordered accummulation of innocent factors leading to disaster" processes

3.17.6.5 Optimalisation processes

3.17.7 An important property of the PEI

One of the features of any process is its duration - its lifespan - LOAO⁴⁸. On the surface, this feature seems to be insignificant, but from our human perspective, the lifespan of biological evolution is extremely important. As a continuous process, biological evolution on our planet has lasted for more than four billion years. For us, it is an unimaginably long time. For this reason, biological evolution is completely nonintuitive for us. We can understand its features only by observations made by mankind in the last few centuries, fossils and analyses such as those presented in this book. We are noty able to see biological evolution in its entirety, reboot it or create a computer simulation, it is just impossible⁴⁹.